Fungsi parametrik adalah fungsi yang dipengaruhi oleh paramater tertentu. misalnya ” t”. Jadi bukan lagi y=f(x) akan tetapi x=f(t) dan y=g(t). Perlunya menggunakan fungsi parametrik adalah karena suatu kurva berubah posisi koordinatnya (x,y) lebih karena dipengaruhi oleh faktor “t”. Sehingga kadang kurva terlihat begitu rumit, model kurva ini dibagi menjadi 4 kelompok
Berikut ini contoh sebuah fungsi parametrik dan bagaimana membuat gambarnya

Untuk membuat gambarnya, lebih mudah untuk membuat tabel 3 kolom seperti dibawah ini kemudian baru digambar. Buatlah titik-titik koordinat (x,y) hasil dari memasukkan nilai “t” ke dalam persamaan f(t) dan g(t), kemudian dilanjutkan dengan membentuk kurva yang mulus

Terlihat dari gambar di atas, adalah sebuah kurva parabola. Dan kita bisa mengetahui persamaan parametrik di atas merupakan persamaan parabola atau bukan, dengan mengeliminasi paramater “t”. Caranya sebagai berikut

Seperti halnya persamaan dalam bentuk y=f(x), maka persamaan parametrik juga bisa diturunkan dan juga diintegralkan. Akan tetapi harus mengikuti beberapa cara berikut
Penurunan Funsi Parametrik

Untuk lebih jelasnya, mari kita perhatikan contoh berikut

2. vektor pada bidang
Atau vector dapat kita definisikan vector adalah ruas garis berarah yang panjang dan arahnya
tertentu.
Suatu vektor terdiri dari panah – panah yang
digambarkan, panah ini memiliki 2 ujung, yaitu titik awal (pangkal) dan titik
akhir (ujung). Vektor adalah besaran yangmempunyai nilai dan arah. Dua vektor
dikatakan ekuivalen jika kedua vektor tersebutmemiliki besaran dan arah yang
sama.
Kita dapat menuliskan vektor tersebut dengan huruf tebal,
seperti u dan v. Besaran dari vector u dilambangkan
dengan |u|.
a. penjumlahan vektor
Cara segitiga
Dalam cara ini, titik pangkal vektor b berimpit ruas dengan titik ujung
vektor a. Jumlah vektor a dan b didapat dengan menarik ruas garis dari
titik pangkal vektor a ke titik ujung vektor b. Ruas garis ini diwakili oleh
vektor c. Akibatnya, a + b = c.
Cara jajargenjang
Misalkan, vektor a mewakili ruas garis berarah dari titik pangkal A ke
titik B dan vektor b mewakili ruas garis berarah dari titik pangkal C ke titik
D. Dalam cara jajargenjang, titik pangkal vektor a berimpit dengan titik
pangkal vektor b, yaitu A= C.
contoh :
Penjumlahan vector menurut aturan segitiga adalah sebagai berikut
Sehingga v+u adalah vector yang diwakili oleh segmen garis berarah yang pangkalnya berimpit
dengan pangkal v dan ujungnya berimpit dengan ujung u yang telah dipindahkan sedemikian
sehingga pangkal u berimpit dengan ujung v.
b. pengurangan vektor
secara geometris, a dan b dapat dikurangkan sebagai berikut
untuk vektor bidang berlaku
dengan menggunakan pasangan terurut, dapat dituliskan
c. perkalian titik/skalar vektor
Maka hasil kali skalar dua vektor dapat ditulis dalam bentuk 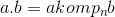 atau
atau adapun sifat-sifat perkalian skalar sebagai
berikut:
adapun sifat-sifat perkalian skalar sebagai
berikut:
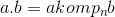 atau
atau adapun sifat-sifat perkalian skalar sebagai
berikut:
adapun sifat-sifat perkalian skalar sebagai
berikut:

























0 komentar:
Posting Komentar