Dua orang Perancis yaitu Pierre Fermat dan Rene Descartes, telah memperkenalkan system koordinat yang sekarang kita kenal dengan sebutan system koordinat Cartesius atau siku-siku. Sistem koordinat ini adalah dasar dari geometri analitik, dan sangat membantu pengembangan kalkulus diferensial dan kalkulus integral yang kita capai hingga saat ini. Dengan memberikan jarak berarah dari dua sumbu yang tegak lurus bukanlah satusatumya jalan untuk menunjukkan kedudukan suatu titik pada bidang. Cara lain adalah menggunakan apa yang disebut koordinat kutub.
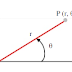
Kita mulai dengan menggambar sebuah setengah-garis tetap yang dinamakan sumbu kutub yang berpangkal pada sebuah titik 0. Titik ini disebut kutub atau titik asal. Biasanya sumbu kutub ini kita gambar mendatar dan mengarah ke kanan dan oleh sebab itu sumbu ini dapat disamakan dengan sumbu x positif pada sebuah system koordinat siku-siku. Setiap titik P (selain dari kutub) adalah perpotongan antara sebuah lingkaran tunggal yang berpusat di 0 dan sebuah sinar tunggal yang memancar dari 0. Jika r adalah jari-jari lingkaran dan θ adalah salah satu sudut antara sinar dan sumbu kutub, maka (r, θ) dinamakan sepasang koordinat kutub dari titik P
koordinat kutub :
P (r, θ)
r : jarak dari O ke P (arah dari O menuju ke P)
θ : sudut antara sumbu x dan garis OPcontoh:
pada gambar diatas ada dua lingkaran yang kecil
berjari-jari 2 dan yang besar berjari-jari 3.Dan juga terdapat dua garis lurus yang
menunjukkan sudut diukur dari sumbu polar.Titik A terdapat pada lingkaran kecil
(r=2) dengan sudut π/4 sehingga dapat dinyatakanA (2, π/4)Titik B terdapat
pada lingkaran besar (r=3) dengan sudut π/2 sehingga dapat dinyatakanB (3, π/2). begitu seterusnya untuk titik C, D, E dan F.
titik pada kordinat polar merupakan titik potong antara jari-jari lingkaran yang berpusat pada titik kutub dan garis arah sudut
jadi titik dengan koordinat Titik asal mempunyai koordinat (-3, π/6) sama saja dengan titik (-3, 13π/6), (3, -11π/6), (-3, 25π/6), (3, 7π/6) dan seterusnya. titik asal mempunyai koordinat (0, θ), di mana θ sudut sembarang.
2. persamaan kutub
Seperti halnya dengan system koordinat siku-siku, kita juga dapat menggambarkan grafik sebuah persamaan kutub. Grafik persamaan kutub adalah himpunan titik-titik yang mempunyai paling sedikit sepasang koordinat kutub yang memenuhi persamaan yang bersangkutan. Salah satu cara untuk menggambar grafik itu adalah dengan menyusun daftar nilai-nilai koordinat, kemudian menggambar titik dengan koordinat-koordinat yang bersangkutan dan akhirnya menghubungkan titik itu dengan sebuah kurva yang mulus.
pada sistem koordinat kartesius siku-siku, dapat disusun persamaan kartesius dengan peubah-peubah x dan y; maka dengan sistem koordinat kutub, dapat pula disusun persamaan kutub dengan peubah-peubah r dan θ.
Contoh 1. :
Gambar grafik persamaan kutub r = 8 sin θ
Penyelesaian :
Kita ganti kelipatan π/6 untuk θ dan menghitung nilai r yang bersangkutan. Apabila
θ naik dari 0 hingga 2π, grafik dilintasi dua kali
contoh 2 :
Gambarlah grafik dari r = 2/1-cos θ
penyelesaian :
Perhatikan gejala yang tidak akan terjadi dengan system
koordinat siku-siku. Koordinat (-2, 3π/2) tidak memenuhi persamaan. Walaupun
demikian titik P (-2, 3π/2) terletak pada grafik, sebab (2, π/2) merupakan koordinat P
dan memang memenuhi persamaan tersebut. Kita dapat menarik kesimpulan bahwa
dalam system koordinat kutub, walaupun ada sepasang koordinat tertentu yang tidak
memenuhi suatu persamaan, tetapi ini tidak perlu mengakibatkan bahwa titik yang
bersangkutan tidak terletak pada grafik persamaan itu. Kenyataan ini mengakibatkan
banyak kesulitan; kita harus belajar terbiasa dengan kenyataan tersebut.
3. hubungan koordinat kutub dan koordinat kartesius
Andaikan sumbu kutub berimpit dengan sumbu x positif system koordinat Cartesius.
Maka koordinat kutub (r, θ) sebuah titik P dan koordinat Cartesius (x, y) titik itu
dihubungkan oleh persamaan :
Hubungan tersebut jelas berlaku untuk sebuah titik P yang berada di dalam kuadran
pertama, yang dapat kita lihat pada Gambar berikut
contoh 1 :
Tentukan koordinat Cartesius dari titik yang koordinat kutubnya adalah (4, π/6).
Tentukan juga koordinat kutub titik yang koordinat Cartesiusnya adalah
Penyelesaian :
Jika (r, θ) = (4, π/6), maka
gambar 8
Ada kalanya grafik persamaan kutub dapat kita lukis dengan mencari persamaannya
dalam system Cartesius. Sebagai contoh kita sajikan kasus di bawah ini
contoh 2 :
Buktikan bahwa grafik persamaan r = 8 sin θ adalah sebuah lingkaran
dan bahwa grafik persamaan r = 2 / (1- cos θ) adalah sebuah parabol
dengan jalan menulis persamaan Cartesius kurva tersebut.
penyelesaian :
Kalikan ruas kiri dan kanan persamaan r = 8 sin θ dengan r, kita peroleh
r2
= 8r sin θ
dalam bentuk Cartesius persamaan tersebut, menjadi :
x2
+ y2 = 8y
dan persamaan ini dapat diubah sebagai berikut :
x2
+ y2 - 8y = 0
x2
+ y2 - 8y + 16 = 16
x2
+ (y - 4)2 = 16
Persamaan terakhir ini adalah persamaan lingkaran yang berpusat di (0, 4) dan
berjari-jari 4.
PERHATIKAN
Karena r bisa bernilai 0, ada kesalahan yang mungkin terjadi dalam mengalikan
kedua sisi pada suatu persamaan kutub dengan r atau dalam membagi kedua
bagian tersebut dengan r. Pada kasus yang pertama, kita dapat menambahkan
kutub pada grafik; pada kasus kedua, kita dapat menghilangkan kutub dari grafik.
Dalam Contoh di atas, kita kalikan kedua sisi dari r = 8 sin θ dengan r tanpa
menimbulkan kesalahan karena kutubnya telah terdapat pada grafik sebagaimana
titik dengan koordinat-θ 0.
Persamaan kedua kita ubah berturut-turut sebagai berikut :
r = 2/1-cos θ
r – r cos θ = 2
r - x = 2
r = x + 2
r2
= x2
+ 4x + 4
x2
+ y2
= x2
+ 4x + 4
y2
= 4(x + 1)
Kita lihat bahwa persamaan terakhir ini adalah persamaan parabol dengan puncak di
(-1, 0) dan dengan fokus di (0, 0)
0 komentar:
Posting Komentar