BAB II GARIS SEBAGAI KURVA BERDERAJAT SATU

  

 2.1 Persamaan Umum Garis, Gradien dan Sudut Inklinasi

Persamaan Umum Garis

Garis dibentuk oleh paling sedikit dua buah titik berbeda. Sebagai suatu himpunan, garis merupakan himpunan titik-titik yang tak hingga dan tak berbatas sehingga garis tidak memiliki dimensi panjang. Jika garis dibentuk oleh titik A dan B maka garis tersebut dapat dinamakan sebagai garis AB. Notasi lain untuk penamaan garis yaitu menggunakan huruf kecil misalnya g, h, l, m dan sebagainya. Sebuah garis juga disebut kurva berderajat satu yang dinyatakan sebagai :

Ax + By + C = 0 untuk A, B, C bilangan riil dan x, y variabel bilangan riil

Sebuah garis dapat ditentukan persamaan kurva berderajat satu seperti di atas apabila diketahui tiga buah titik yang dilalui oleh garis tersebut. 

Contoh 1

Sebuah garis yang melalui titik A(1, 2), B(-3, 4), dan C(5, 0) maka persamaan kurva berderajat satu untuk garis tersebut ditentukan sebagai berikut. 

Langkah 1) Substitusi koordinat titik ke dalam persamaan kurva

Garis melalui A(1, 2) ⇒ A(1) + B(2) + C = 0 ⇒ A + 2B + C = 0 ---------------------------- pers. 1

Garis melalui B(-3, 4) ⇒ A(3) + B(-4) + C = 0 ⇒ -3A + 4B + C = 0 ------------------------ pers. 2

Garis melalui C(5, 0) ⇒ A(5) + B(0) + C = 0 ⇒ 5A + C = 0 --------------------------------- pers. 3

Langkah 2) Membuat sistem persamaan linier tiga variabel −𝐴+2𝐵+𝐶=03𝐴+4𝐵+𝐶=05𝐴+𝐶=0

Langkah 3) Menyelesaikan sistem persamaan linier

Penyelesaian sistem persamaan linier di atas yaitu :

A = 1, B = 2 dan C = -5

Maka persamaan kurva berderajat satu untuk garis yang melalui A(1, 2), B(-3, 4), dan C(5, 0) yaitu x + 2y - 5 = 0

Gradien dan sudut inklanasi

Garis x + 2y - 5 = 0 seperti ditunjukkan pada gambar di atas membentuk sudut terhadap sumbu x positif. Besarnya sudut yang terbentuk tersebut akan mempengaruhi kemiringan garis. Sudut bernilai positif yang dibentuk antara garis dan sumbu x positif dinamakan sudut inklinasi garis (angle of inclination) dan biasanya dinotasikan oleh sudut 

Gradient atau kemiringan suatu garis adalah besarnya sudut yang dibentuk oleh garis tersebut terhadap garis horizontal. Besarnya kemiringan dimulai dari negatif tak hingga dan sampai menuju tak terhingga. gradien (slope of the line) dinyatakan oleh notasi m.

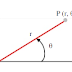
Nilai gradien suatu garis dapat bernilai positif, negatif, nol atau tidak terdefinisi. Gradien suatu garis dapat ditentukan dengan menggunakan konsep trigonometri pada segitiga siku-siku namun dengan memperhatikan interval nilai sudut yang dibentuk oleh garis terhadap sumbu x positif. Perhatikan gambar sebuah garis berikut. Garis tersebut melalui dua titik yaitu P1(x1, y1) dan P2(x2, y2). Sudut yang dibentuk garis P1P2 adalah α. Pada gambar terlihat sebuah segitiga siku-siku dengan hipotenusa P1P2, panjang sisi alas x2 - x1 dan panjang sisi tegak y2 - y1. Nilai tangent sudut α dapatditentukan sebagai perbandingan antara panjang sisi tegak terhadap panjang sisi alas segitiga siku-siku. Sehingga dapat dirumuskan :

Jadi nilai gradien suatu garis merupakan nilai tangen sudut inklinasi dan besarnya sudut inklanasi adalah nilai arc tan dari gradien garis.

Bentuk persamaan kurva berderajat satu dapat diubah menjadi fungsi dari x di mana x adalah variabel bebas dan y adalah variabel terikat sebagai berikut :

Konstanta m disebut sebagai gradien yang menunjukkan kemiringan garis dan c merupakan konstanta persamaaan. Persamaan y = mx + c disebut persamaan garis bergradien m.

Contoh 2

Persamaan kurva berderajat satu pada contoh 5 dapat diubah menjadi persamaan garis bergradien dengan langkah sebagai berikut.

x + 2y - 5 = 0 ⇒ 2y = -x + 5 ⇒ 𝒚= −𝟏𝟐𝒙+ 𝟓𝟐

maka gradien garis yang melalui titik A(1, 2), B(-3, 4), dan C(5, 0) adalah m = - ½ yaitu bergradien negatif. Sudut inklinasi yang dibentuk garis tersebut yaitu :

𝜶=𝒂𝒓𝒄 𝒕𝒂𝒏 (−𝟏𝟐)≈−𝟎,𝟒𝟔𝟒 𝒓𝒂𝒅 ≈ −𝟐𝟔,𝟓𝟕° ≈𝟏𝟓𝟑,𝟒𝟑°

Pertanyaan 3 - 1 : Deskripsikan bentuk masing-masing garis berdasarkan gradien dan sudut inklinasi yang ditunjukkan pada gambar berikut.

Penyelesaian :

Diketahui : Empat garis berbeda p = AB, q = AC, r = BC, dan s = BD

Ditanyakan : Bentuk garis p, q, r dan s berdasarkan gradien dan sudut inklinasi … ?

Identifikasi masalah : Tiap garis melalui paling sedikit dua titik berbeda. Jika diketahui koordinat kedua titik yang dilalui garis maka dapat ditentukan persamaan garis bergradien dengan menggunakan metode penyelesaian sistem persamaan linier dua variabel. Atau dapat menggunakan konsep trigonometri pada segitiga siku-siku untuk menentukan gradien suatu garis. Sebagai contoh garis p = AB melalui titik A(1, 1) dan B(5, 4). Ruas garis 𝐴𝐵̅̅̅̅ merupakan hipotenusa dari segitiga siku-siku ADB. Kemiringan garis AB membentuk sudut  BAD

sehingga kemiringan garis dapat ditentukan dari nilai tangen ukuran sudut  BAD 𝒎= 𝐭𝐚𝐧∡ 𝑩𝑨𝑫= |𝑫𝑩̅̅̅̅̅||𝑨𝑫̅̅̅̅|

Sudut inklanasi garis ditentukan dengan mencari nilai arc tan dari gradien.

Langkah penyelesaian :

Cara 1 : Metode penyelesaian sistem persamaan linier dua variabel (SPLDV) untuk garis r = BC yang melalui titik B(5, 4) dan C(7, 1)

Langkah 1 : Substitusi koordinat titik-titik ke dalam persamaan garis y = mx + c

Garis melalui titik B ⇒ 4 = 5m + c

Garis melalui titik C ⇒ 1 = 7m + c

Langkah 2 : Metode eliminasi SPLDV 

4 = 5m + c

1 = 7m + c -

3 = -2m

𝑚= −32 

4 = 5m + c | x 7 28 = 35m + 7c

1 = 7m + c | x 5 5 = 35m + 5c -

23 = 2c

𝑐=232

Langkah 3 : Substitusi nilai m dan c ke dalam persamaan garis y = mx + c

Persamaan garis yaitu 𝑦=−32𝑥+232

Cara 2 : Metode pencarian nilai tangen sudut yang dibentuk hipotenusa segitiga siku-siku untuk garis r = BC yang melalui titik B(5, 4) dan C(7, 1)

Langkah 1 : Membuat segitiga siku-siku dengan hipotenusa adalah ruas garis dari dua titik pada garis
Segitiga siku-siku yang dapat dibuat dengan hipotenusa BC̅̅̅̅ yaitu segitiga BDC. 

Langkah 2 : Menentukan panjang sisi alas dan sisi tegak segitiga

Sisi alas segitiga BDC adalah 𝐷𝐶̅̅̅̅ dan sisi tegak segitiga BDC adalah 𝐵𝐷̅̅̅̅ . Panjang masing-masing ruas garis dicari dengan menggunakan rumus jarak antara dua titik. |𝐷𝐶̅̅̅̅|=√(5−7)2+(1−1)2=2

|𝐵𝐷̅̅̅̅|=√(5−5)2+(4−1)2=3

Langkah 3 : Menentukan nilai tangen sudut yang dibentuk oleh hipotenusa segitiga siku-siku

Sudut yang dibentuk antara hipotenusa 𝐵𝐶̅̅̅̅ dan sisi alas 𝐷𝐶̅̅̅̅ yaitu DCB. Berdasarkan gambar di atas dapat dilihat bahwa DCB berada di kuadran II yaitu pada interval 90 <   180 atau 𝜋2<𝜃≤𝜋. Oleh karena itu nilai tangent sudut pada kuadran tersebut adalah negatif. Maka nilai dari tangent sudut tersebut dicari sebagai berikut. 𝑚=tan∡ 𝐷𝐶𝐵= −|𝐵𝐷̅̅̅̅||𝐷𝐶̅̅̅̅|=− 32

Langkah 4 : Menentukan besar sudut inklinasi

Sudut inklinasi garis r = BC yaitu : 𝛼=𝑎𝑟𝑐tan𝑚=𝑎𝑟𝑐tan(−32)≈−0,983 𝑟𝑎𝑑 ≈ −56,31° ≈123,69°

Langkah 5 : Deskripsi bentuk garis berdasarkan gradient dan sudut inklinasi

Garis r memiliki gradien 𝑚= −32 yaitu bergradien negatif yang ditunjukkan dengan bentuk garis dari kiri atas ke kanan bawah dengan besar sudut inklinasi membentuk sudut tumpul sekitar 123,69. Hasil pencarian gradien masing-masing garis p, q, r, dan s diringkas sebagai berikut.

Tabel 1. Hubungan antara gradien, sudut inklinasi, dan bentuk garis

Sifat-sifat Garis dalam Bidang : Kesejajaran dan Perpotongan 

Sifat-sifat garis yang berada dalam sebuah bidang dalam geometri Euclide meliputi garis-garis yang berpotongan atau tidak berpotongan. Dua buah garis dikatakan berpotongan jika ada sebuah titik potong yang dilalui kedua garis. Dua garis tidak berpotongan disebut saling sejajar. Perhatikan bentuk garis-garis pada gambar berikut

Gambar di atas memperlihatkan bahwa garis-garis bergradien positif atau negatif memotong sumbu x dan sumbu y masing-masing di satu titik. Perpotongan garis tersebut dengan sumbu x ditentukan dengan mensubstitusikan nilai y = 0 ke dalam persamaan garis. Perpotongan garis tersebut dengan sumbu y ditentukan dengan cara mensubstitusikan nilai x = 0 ke dalam persamaan garis. Sedangkan garis sejajar sumbu x hanya memotong sumbu y dan tidak memotong sumbu x. Garis sejajar sumbu y hanya memotong sumbu x dan tidak memotong sumbu y.Tabel berikut meringkas hubungan persamaan garis dan titik-titik potong garis terhadap sumbu x dan sumbu y.