BAB I TITIK DAN KURVA PADA SISITEM KOORDINAT CARTESIUS

Geometri… hmmmmmm.. ketika mendengar kata ini pasti yang terbayang di pikiran kalian adalah bentuk, bangun, ruang, dan sebagainya.. tapi apa ada yang tau apa yang dimaksud dengan geometri analitik dan apa saja yang di pelajari dalam geometri analitik.. yukk mari kita baca bahasannya secara lengkap dibawah ini….

1.   Pengertian  geometri analitik

Geometri (Greek; geo= bumi, metria= ukuran) adalah sebagian dari matematika yang mengambil persoalan mengenai ukuran, bentuk, dan kedudukan serta sifat ruang. Geometri adalah salah satu dari ilmu yang tertua. Adapun Geometri analitik adalah suatu cabang ilmu matematika yang merupakan kombinasi antara aljabar dan geometri. Dengan membuat korespondensi antara persamaan matematika secara aljabar dengan tempat kedudukan secara geometric diperoleh suatu metoda pemecahan masalah geometri yang lebih sistematik dan lebih tegas.

 Perkembangan geometri analitik dimulai dengan kehadiran bentuk baru persamaan (equation) Bentuk baru persamaan tersebut memungkinkan untuk mengklasifikasikan kurva berdasarkan derajat (degree). Kurva berderajat satu adalah garis lurus (straight lines), kurva berderajat dua merupakan irisan kerucut (conic sections), dan kurva berderajat tiga dinamakan kurva kubik (cubic curves).

2. Garis bilangan

Persekutuan antara aljabar dan geometri adalah membuat pengaitan antara bilangan dalam aljabar dengan titik dalam geometri. Misalkan kita perhatikan pengaitan bilangan dengan titik pada sebuah garis yang tidak terbatas pada kedua arahnya.

Misalkan kita perhatikan pengaitan bilangan dengan titik pada sebuah garis yang tidak terbatas pada kedua arahnya. Pertama-tama, kita pilih pasangan titik O dan P pada garis seperti terlihat pada gambar 1.1.

Titik O disebut pusat, yaitu dikaitkan dengan bilangan nol, dan titik P yang terletak di sebelah kanan O dikaitkan dengan bilangan satuan. Dengan menggunakan OP sebagai panjang satuan, kita kaitkan bilangan-bilangan lain dengan semua titik pada garis dengan cara berikut; Titik Q yang terletak satu sisi dengan P terhadap titik pusat O dikaitkan dengan bilangan positif x jika dan hanya jika jarak dari titik pusat adalah x, yaitu OQ = xOP . Titik R yang terletak berlawanan sisi dari titik pusat dikaitkan dengan bilangan negatif – x jika dan hanya jika jarak dari titik pusat adalah x.

Dengan cara ini setiap titik pada garis dikaitkan dengan satu bilangan real, dan untuk setiap bilangan real berkorespondensi dengan sebuah titik pada garis. Suatu garis yang titik-titiknya dikaitkan dengan bilangan-bilangan real disebut garis bilangan. Skala yang dijelaskan pada garis bilangan disebut koordinat garis. Bilangan yang menyatakan suatu titik yang diberikan disebut koordinat titik tersebut, dan titik itu disebut grafik dari bilangan.

3.   System koordinat

Titik-titik pada sebuah garis (pada ruang dimensi satu) dinyatakan dengan bilangan tunggal. Sedangkan titik-titik pada sebuah bidang (ruang dimensi dua) dapat dinyatakan dengan pasangan suatu bilangan. Lebih lanjut untuk titik-titik di ruang dimensi tiga dapat dinyatakan dengan tripel suatu bilangan. Untuk merepresentasikan titik pada sebuah bidang dengan pasangan bilangan, kita tentukan dua garis bilangan bersilangan OX dan OY, dan tentukan skala pada masing-masing garis, seperti pada gambar 1.2. Titik potong kedua garis itu digunakan sebagai titik pusat. Bilangan positif ditempatkan pada sebelah kanan titik O garis mendatar OX dan sebelah atas titik O garis ke vertikal OY. Sedangkan bilangan negatif ditempatkan pada sebelah kiri titik O garis mendatar OX dan sebelah bawah titik O garis ke vertikal OY. Biasanya arah positif ditandai dengan tanda panah pada garis bilangan. Garis OX disebut sumbu-x dan garis OY disebut sumbu-y. Dua garis yang bersilangan itu disebut sumbu koordinat.

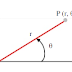
Misalkan diberikan sebuah titik P pada bidang yang diberi sumbu koordinat, maka terdapat korespondensi dengan titik Px pada sumbu x. Ini adalah titik potong antara sumbu x dengan garis yang sejajar sumbu y yang memuat titik P (jika P berada pada sumbu y maka garis ini berimpit dengan sumbu y). Dengan cara yang sama terdapat titik Py pada sumbu y, yang merupakan titik potong sumbu y dengan garis yang melalui titik P dan sejajar (atau sama) dengan sumbu x. Koordinat kedua titik pada sumbu disebut koordinat titik P. Jika a adalah koordinat Px pada sumbu-x dan b adalah koordinat Py pada sumbu-y maka P direpresentasikan dengan (a, b) atau P(a, b). Dalam contoh ini, a disebut koordinat x, atau absis dari P, dan b disebut koordinat y, atau ordinat dari P. Pada saat sebuah titik tertentu diberikan, meskipun nilai numerik dari komponen koordinatnya tidak diketahui, maka koordinat itu biasanya dinyatakan dengan notasi x dan y yang berindeks atau dengan huruf-huruf awal dari alpabet. Sebagai contoh P1(x1,y1) atau P(a, b).

Pada bidang koordinat, biasanya disepakati aturan sebagai berikut:

(1) sumbu-sumbu koordinat diambil yang tegak lurus satu sama lain;

(2) sumbu x adalah garis mendatar (horisontal) dengan koordinat positif arah kanan dari titik pusat, dan sumbu y adalah garis vertikal dengan koordinat positif ke arah atas dari titik pusat koordinat;

(3) digunakan skala yang sama pada kedua sumbu koordinat. Kesepakatan ini tentu saja, tidak harus diikuti semuanya jika ada pilihan yang lebih menguntungkan.

Kita harus sering meninjau kesepakatan ketiga yaitu apabila akan menentukan gambar akan sangat sulit membuat sketsa grafik jika kita tetap menggunakan skala yang sama pada kedua sumbu. Pada kasus seperti ini, kita harus merasa bebas menggunakan skala yang berbeda, mengingat penyimpangan gambar yang terjadi dalam proses. Kecuali tetap memegang kesepakatan atau dinyatakan dalam keadaan tertentu, atau jelas dinyatakan dalam konteks, biasanya kita selalu mengikuti dua kesepakatan pertama. Sumbu-sumbu koordinat memisahkan bidang ke dalam empat daerah, yang disebut kuadran. Biasanya kuadran diidentifikasi dengan angka romawi sebagaimana ditunjukkan dalam gambar 1.3. Titik-titik pada sumbu-sumbu koordinat tidak masuk pada sembarang kuadran. Urutan tanda dari absis dan ordinat (x, y) ditunjukkan dalam gambar 1.3.

Dalam sistem koordinat tegaklurus setiap pasangan berurutan dari bilangan real dinyatakan dengan satu dan hanya satu titik pada bidang koordinat, dan setiap titik pada bidang koordinat berkorespondensi satu dan hanya satu pasangan berurutan dari bilangan real. Koordinat titik-titik yang ditentukan dengan cara ini, seringkali dikenal sebagai koordinat Cartesius, sebagai penghormatan terhadap matematikawan dan filosof asal Perancis yang bernama René Descartes yang hidup dari 1596 sampai 1650. Satu hal yang perlu dicatat adalah dua garis sumbu koordinat tidak perlu harus berpotongan secara tegak lurus. Namun demikian jika kedua sumbu berpotongan miring, hasil-hasil secara aljabar menjadi lebih rumit.

4.   Plotting

           Proses lokalisasi dan pemberian tanda sebuah titik yang koordinatnya diberikan disebut plotting titik. Untuk melakukan plotting telah banyak disediakan kertas grafik yang berupa kertas berpetak persegi kecil-kecil. Gambar 1.4. menyatakan plotting beberapa titik pada bidang. Sekarang kita dapat mengidentifikasi koordinat dari titik-titik dalam gambar 1.4. Perhatikan bahwa semua titik pada sumbu x mempunyai ordinat nol, dan juga titik-titik pada sumbu y mempunyai absis nol sebab keduanya berada pada sumbu koordinat.

          5. Jarak antara dua titik 

Telah kita kaitkan titik-titik dengan koordinat. Sekarang akan kita pergunakan untuk menyelesaikan masalah geometri. Kita mulai dengan konsep jarak antara dua titik. Konsep titik diperkenalkan dalam geometri Euclid sebagai elemen yang tidak didefinisikan dan tidak memiliki dimensi panjang. Euclid mendefinisikan titik dalam buku I - Element yaitu “a point is that which has no part”. Geometri Euclid hanya membahas sifat titik yang diam/tetap, sedangkan geometri analitik juga menelaah sifat-sifat titik yang bergerak seperti yang terjadi di alam. 

Misalnya sebuah bola yang menggelinding pada permukaan bidang miring dapat dinyatakan sebagai sebuah titik yang bergerak sehingga titik tersebut mengalami perpindahan tempat. Posisi bola saat di bagian atas tidak sama dengan posisi bola saat berada di pertengahan bidang. Proses menelaah sifat titik-titik di berbagai posisi tersebut maka dibutuhkan bantuan aljabar untuk menyatakan posisi titik dalam suatu simbol tertentu.

Gambar 7. Representasi Titik yang Berpindah posisi

Metode yang digunakan untuk menunjukkan posisi sebuah titik pada sebuah bidang mirip seperti teknik menggambar peta. Posisi suatu tempat pada permukaan bumi dinyatakan oleh koordinat peta yaitu derajat lintang (arah utara atau selatan) dan derajat bujur (arah timur atau barat). Posisi acuan untuk koordinat bujur-lintang tersebut yaitu Kota Greenwich di Inggris. Perhatikan gambar dan penjelasan di bawah ini. Misalkan kurva NGAS adalah meridian utama, kurva AWBE adalah garis ekuator, dan titik G adalah kota Greenwich maka posisi kota P dapat dinyatakan sebagai koordinat peta apabila derajat AB dan BP diketahui. Andaikan AB = 70° dan BP = 45° maka posisi P dinyatakan sebagai 70° bujur timur dan 45° lintang utara

Gambar 8. Representasi Koordinat Peta

Geometri analitik menyederhanakan koordinat peta tersebut dengan menggunakan dua garis lurus berpotongan untuk menggantikan kurva meridian dan kurva ekuator. Titik potong kedua garis dijadikan sebagai titik acuan biasanya dinyatakan sebagai titik O. Posisi titik P dinyatakan oleh panjang ruas garis BP yang sejajar dengan garis sumbu X¢X dan panjang ruas garis AP yang sejajar garis sumbuYY¢. Panjang ruas garis BP sama dengan panjang ruas garis OA. Panjang ruas garis AP sama dengan panjang ruas garis OB. Sehingga titik P dapat dinyatakan berada pada posisi sejauh panjang OA dan OB terhadap titik O. 
 

Gambar 9. Representasi Titik dalam Sistem Koordinat

Dua buah titik berbeda akan berada pada posisi yang berbeda. Jarak kedua titik tersebut dapat ditentukan dengan langkah-langkah sebagai berikut :

(1)    Buatlah dua titik berbeda yaitu A dan B lalu hubungkan dengan sebuah ruas garis.

(2)    Buat sebuah garis melalui A dan sebuah garis lain yang melalui B sehingga kedua garis berpotongan tegak lurus.

(3)    Tentukan titik potong kedua garis yaitu C sehingga diperoleh segitiga siku-siku ACB atau BCA lalu ukur panjang ruas garis CA dan CB

(4)  Tentukan panjang ruas garis AB dengan menggunakan Teorema Phytagoras : 

Titik-titik pada sebuah bidang yang membentuk himpunan titik dan memenuhi suatu kriteria tertentu dinamakan kedudukan titik (locus of points). Kedudukan titik dapat dinyatakan sebagai suatu fungsi. Misalnya titik-titik pada lingkaran berjari-jari 1 cm dapat dinyatakan sebagai x² + y² = 1. Secara geometris, hanya titik-titik berjarak 1 cm dari titik pusat lingkaran tersebut yang memenuhi kedudukan titik yang dinyatakan oleh persamaan x² + y² = 1. 




6.   Teorema dasar tentang kedudukan titik

Teorema-teorema dasar tentang kedudukan titik-titik (Fundamental Locus Theorems)  adalah sebagai berikut. 

Teorema 1.1

Kedudukan titik-titik yang berjarak sama yaitu d dari sebuah titik P adalah sebuah lingkaran berpusat di titik P dengan ukuran panjang jari-jari d

Teorema 1.2

Kedudukan titik-titik yang berjarak sama yaitu d dari sebuah garis l  adalah sepasang garis-garis sejajar yang masing-masing berjarak d dari garis l

Teorema 1.3
Kedudukan titik-titik yang berjarak sama (equidistant) dari dua buah titik P dan Q adalah sebuah ruas garis (disebut perpendicular bisector).yang tegak lurus  terhadap ruas garis dan membagi menjadi dua bagian sama besar 

 Teorema 1.4
Kedudukan titik-titik yang berjarak sama dari dua garis yang sejajar yaitu l₁ dan l₂ merupakan sebuah garis diantara keduanya dan sejajar dengan kedua garis tersebut.

 Teorema 1.5

Kedudukan titik-titik yang berjarak sama terhadap dua garis yang berpotongan yaitu l₁ dan l₂, adalaha sepasang ruas garis (disebut bisectors) yang membagi dua sama besar sudut-sudut yang yang dibentuk garis l₁ dan l₂

Teorema 1.6

Kedudukan titik-titik yang berjarak sama dari kedua sisi sebuah sudut adalah sebuah ruas garis yang membagi dua sudut tersebut (bisector of angle)

Teorema 1.7

Kedudukan titik-titik yang berjarak sama dari dua buah lingkaran konsentris (concentric circles) adalah sebuah lingkaran yang konsentris terhadap kedua lingkaran tersebut dan berada tepat di tengah keduanya

Teorema 1.8

Kedudukan titik-titik pada jarak tertentu dari sebuah lingkaran yang memiliki jari-jari lebih panjang dari jarak tersebut merupakan sebuah pasangan lingkaran konsentris, di mana masing-masing kedudukan titik tersebut berada di salah satu sisi lingkaran pada jarak tertentu tersebut.

Teorema 1.9

Kedudukan titik-titik yang berjarak tertentu dari suatu lingkaran berjari-jari kurang dari jarak tersebut merupakan sebuah lingkaran yang berada di luar lingkaran pertama dan saling konsentris. 

Contoh pembuktian teorema

Tahap 1     : Akan dibuktikan untuk sembarang titik pada kedudukan tersebut memenuhi kondisi-kondisi berikut :

Diketahui    : Titik A dan B ruas garis tegak lurus dan membagi ruas garis 

Ditanyakan  : Apakah untuk sembarang titik P pada ruas garis  berjarak sama dari A dan B yaitu?

 Bukti tahap 1

Pernyataan	Alasan
1.     adalah ruas garis membagi dua dan tegak lurus  2.    Ukuran sudut PEA dan sudut PEB sama yaitu 3. Ukuran panjang ruas garis  4.     5.     6.	1.    Diketahui 2.    Kedua sudut adalah sudut siku-siku. Semua sudut siku-siku kongruen 3.    Agar dapat membagi dua sama besar maka ruas garis dibagi menjadi bagian-bagian yang kongruen 4.    Sifat refleksif 5.    Kekongruenan dua segitiga (s.a.s) 6.    Hukum kongruensi

7.   Pemecahan masalah polya

Pemecahan masalah (problem solving) merupakan suatu prosedur untuk menemukan penyelesaian yang tepat atas suatu masalah. Prosedur tersebut pertama kali diformulasikan oleh George Polya (1887 - 1985) seorang guru dan ahli matematika yang menyatakan bahwa ada empat tahap pemecahan masalah yaitu :  understand the problem, devise a plan, carry out the plan, dan look back sebagai berikut :

1)     Understanding the Problem

Tahap pertama yang dilakukan untuk memecahkan masalah adalah memahami masalah. Cara yang disarankan Polya untuk memahami masalah dengan baik yaitu dengan menjawab pertanyaan-pertanyaan berikut :

a.     Nyatakan masalah dengan kalimatmu sendiri !

b.     Tentukan apa saja yang akan ditemukan/dicari/diselesaikan !

c.     Apa saja yang tidak diketahui dari permasalahan itu ?

d.     Informasi apa saja yang kamu peroleh dari permasalahan itu ?

e.     Informasi apa saja yang tidak ada / hilang dari permasalahan itu ?

f.      Informasi apa saja yang tidak dibutuhkan dari permasalahan itu ?

2)     Devising a Plan

Tahap kedua pemecahan masalah adalah menentukan rencana penyelesaian berupa strategi-strategi pemecahan masalah. Beberapa strategi pemecahan masalah antara lain :

a.     Menemukan pola

b.     Menguji masalah yang relevan dan memeriksa apakah teknik yang sama dapat digunakan untuk menyelesaikan permasalahan

c.     Menguji masalah yang lebih sederhana atau khusus dari permasalahan itu dan diperbandingkan dengan penyelesaian masalah sebenarnya

d.     Membuat tabel

e.     Membuat diagram / gambar

f.      Menebak dan memeriksa (guess and check / trial and error)

g.     Menggunakan persamaan (equation) matematika

h.     Bekerja mundur (work backward)

i.      Mengidentifikasi bagian dari hasil (subgoal)

3)     Carrying Out the Plan

Tahap ketiga pemecahan masalah terdiri dari tiga aktivitas yaitu :

a.     Menerapkan satu atau lebih strategi pemecahan masalah untuk menemukan penyelesaian atau perhitungan

b.     Memeriksa setiap langkah strategi yang digunakan baik secara intuitif maupun dengan bukti formal

c.     Menjaga keakuratan proses pemecahan masalah

4)     Looking Back

Langkah terakhir pemecahan masalah adalah memeriksa kembali jawaban atau solusi terhadap permasalahan sebenarnya dengan cara :

a.     Memeriksa dengan pembuktian

b.     Menginterpretasikan penyelesaian/solusi berdasarkan permasalahan berdasarkan rasional atau pun argumentasi (reasonable)

c.     Jika memungkinkan lakukan pengujian untuk masalah lain yang relevan atau pun yang lebih umum dengan menggunakan teknik/strategi pemecahan masalah tersebut

Contoh 1

Terdapat dua buah pelampung pada sebuah danau. Seorang perenang berenang di danau tersebut sedemikian sehingga ia selalu berjarak tetap (konstan) terhadap kedua pelampung tersebut. Deskripsikan jalur renang yang ditempuh oleh perenang tersebut.

Tahap pemecahan masalah :

1)      Understanding the Problem

a.     Nyatakan masalah dengan kalimatmu sendiri !

Misalkan kedua pelampung adalah titik A dan B dan perenang adalah titik C

Misalkan jarak C ke A adalah d_AC dan jarak C ke B adalah d_CB.

Maka posisi perenang yaitu C terhadap A dan B adalah kumpulan titik-titik sehingga d_CA dan d_CB selalu tetap. Berbentuk apakah kumpulan  titik-titik tersebut ?

b.     Tentukan apa saja yang akan ditemukan/dicari/diselesaikan !

Bentuk kumpulan titik-titik sehingga d_CA dan d_CB selalu tetap.

c.     Apa saja yang tidak diketahui dari permasalahan itu ?

Jarak titik A ke B

d.     Informasi apa saja yang kamu peroleh dari permasalahan itu ?

Titik A dan B berbeda posisi

Jarak d_CA dan d_CB selalu tetap yaitu d_CA = d_CB untuk meskipun posisi C berubah-ubah

2)     Devising a Plan

Strategi pemecahan masalah yang mungkin dapat digunakan untuk menyelesaikan masalah :

a.     Membuat diagram / gambar

Menggambarkan posisi titik A, B, dan C sesuai kondisi masalah.

b.     Menguji masalah yang relevan dan memeriksanya apa dapat digunakan

Memeriksa jika ada satu atau lebih teorema dasar kedudukan titik yang menyerupai masalah ini.

3)     Carrying Out the Plan

a.   Membuat diagram / gambar 

b.     Memeriksa jika ada teorema kedudukan titik yang sesuai

Teorema 2.3 : Kedudukan titik-titik yang berjarak sama (equidistant) dari dua buah titik P dan Q adalah sebuah ruas garis (disebut perpendicular bisector).yang tegak lurus  terhadap ruas garisdan membagi menjadi dua bagian sama besar

Berdasarkan gambar dan teorema tersebut maka kedudukan perenang terhadap kedua pelampung tersebut dapat dideskripsikan sebagai sebuah ruas garis yang tegak lurus terhadap ruas garis yang menghubungkan kedua pelampung yaitu

 

dan membagi ruas garis

 

menjadi dua bagian sama panjang seperti digambarkan sebagai berikut.

4)     Looking Back

Langkah terakhir pemecahan masalah adalah memeriksa kembali jawaban atau solusi terhadap permasalahan sebenarnya dengan cara :

a.     Memeriksa dengan pembuktian : buktikan teorema 2.3 berdasarkan masalah tersebut secara deduktif

b.     Menginterpretasikan penyelesaian permasalahan ini berdasarkan argumentasi (reasonable) dengan menggunakan koordinat dan aljabar

Misalkan koordinat titik C(x, y) di mana d_CA = d_CB dengan koordinat A(x_a, y_a) dan B(x_b, y_b) maka dapat dibuktikan untuk posisi C di C₁(x₁, y₁), C₂(x₂, y₂), … Cn(x_n, y_n) yaitu : (a) jika ruas garis tegak lurus sumbu x maka y₁ = y₂ = … = y_n

(b) jika ruas garis tegak lurus sumbu y maka x₁ = x₂ = … = x_n

Selanjutnya harus dibuktikan bahwa garis C₁C₂ tegak lurus Dengan bantuan geogebra dapat dilakukan simulasi untuk menunjukkan solusi  untuk tiga posisi C yang berbeda-beda sebagai berikut.