Lingkaran
Lingkaran didefinisikan sebagai
himpunan titik-titik yang berjarak sama terhadap suatu titik tertentu. Dapat
juga dikatakan,lingkaran adalah tempat kedudukan titik-titik yang berjarak sama
terhadap suatu titik tertentu. Jarak yang sama itu disebut jari-jari lingkaran
dan titik tertentu itu disebut titik pusat lingkaran.
Berdasarkan
definisi itu, dapat ditentukan persamaan lingkaran.
Jika titik pusat lingkaran adalah [0,0] dan jari-jari lingkaran adalah r maka kita gunakan rumus
jika Pergeseran titikpusat lingkaran sejauh a kearah sumbu-x dan
sejauh b ke arah sumbu-y Persamaan umum lingkaran berjari-jari r berpusat di (a,b) maka rumus yang digunakan
contoh:
Bentuk
Umum Persamaan Lingkaran
Dari persamaan lingkaran dengan
pusat P(a,b) dan berjari-jari r, yakni
Diperoleh
yang dapat ditulis
Ini adalah bentuk umum persamaan
lingkaran. Persamaan ini dapat juga ditulis sebagai berikut
Perhatikan bahwa ini adalah persamaan
lingkaran dengan pusat P
dan berjari-jari r
Dengan memperhatikan nilai r ini,
maka akan tercdapat beberapa kemungkinan jenis lingkaran sebagai berikut
jika
jika
jika
Persamaan Parameter Suatu Lingkaran
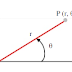
Pada gambar di atas, koordinat titik
T(x, y) yang terletak pada lingkaran dengan pusat P(a, b) dan berjari-jari r
akan memenuhi persamaan berikut ini.
Dalam hal ini,a adalah suatu parameter. Dikatakan, persamaan diatas adalah
persamaan parameter suatu lingkaran.Secara lebih jelas, dengan mengeliminasi
parameter a akan diperoleh persamaan
sebagai berikut.
Garis Singgung
1. garis singgung pada lingkaran dengan titik singgung tertentu
MisalT (x1 ,
y1 ) adalah titik singgung pada lingkaran. Garis singgung g yang melalui
T (x1 ,
y1 ) berbentuk y – y1 = m(x – x1). Karena garis singgung ini tegak lurus dengan jari- jari OT , maka nilai gradien garis singgung ini adalah
m = - x1 /y1 . Sehingga persamaan garis singgung yang dimaksud adalah :
jari OT , maka nilai gradien garis singgung ini adalah
m = - x1 /y1 . Sehingga persamaan garis singgung yang dimaksud adalah :
Karena
titik T (x1 , y1 ) terletak pada lingkaran,
maka dipenuhi x1 + y1 = r Dengan demikian persamaan garis singgung pada lingkaran
x 2 + y 2 = r 2 dengan titik singgung T (x1 ,
y1 )
adalah:
2. Garis Singgung Pada lingkaran dengan Gradien yang telah ditentukan
Persamaan garis lurus dengan gradien m dinyatakan
dengan g: y = mx + n. Jika garis
ini dipotongkan dengan lingkaran L: x 2 + y 2 = r 2 , didapat
x2 +
(mx + n)2 = r2
atau
(m2 + 1)x2 +
2mnx + n2 – r2 =
0…………….. (*)
Ini adalah
persamaan
kuadrat dalam
x. Garis
g
akan
menyinggung lingkaran
L: x 2 + y 2 = r 2 bila diskriminan persamaan (*) adalah nol, yakni
D = 4m 2 n 2 - 4(1 + m 2 )(n 2 - r 2 )
= - 4(n 2 - r 2 - m 2 r 2 ) = 0
Atau
Dengan mensubtitusikan nilai r ini ke persamaan garis g, akan diperoleh persamaan
garis singgung pada lingkaran L x 2 + y 2 = r 2 dengan gradien m, yakni:
Sebagai latihan, dengan cara serupa, tunjukkan bahwa persamaan garis singgung pada
lingkaran (x - a )2 + (y - b)2 = r 2 dengan gradien m adalah:
3. Garis Singgung dari Suatu Titik di luar lingkaran
Misal titik T(x1, y1) adalah titik di luar lingkaran dan
S(x0 , y0 ) adalah titik singgung pada lingkaran. Persamaan garis singgung yang elalui S(x0 , y0 ) adalah:
xx0 + yy 0 = r2……………………. (i)
Garis singgung ini melalui T(x1, y1), sehingga berlaku
x1 x0 + y1 y 0 = r2………………….. (ii)
Karena S(x0 , y0 ) terletak pada lingkaran x 2 + y 2= r 2 maka dipenuhi
Xo 2 + yo 2= r 2 ……………………. (iii)
Dengan menyelesaikan persamaan (ii) dan (iii) akan didapat nilai x0 dan y0 .
Setelah
nilai x0 dan y0 ini disubtitusikan ke
persamaan (i), akan diperoleh persamaan garis singgung
pada lingkaran x 2 + y 2= r
2 yang melalui titik T(x , y ).



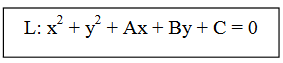























0 komentar:
Posting Komentar